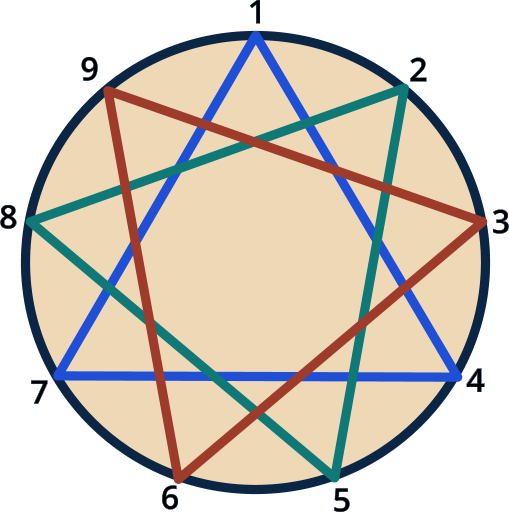
Foundational Terms for Puleo Numbers
Mathematical
Digital Compression
Digital Compress is the process of adding the digits of a number together to arrive at a single digit. For Example, take the number 4896. Add 4+8+9+6 = 27, 2+7=9
Digital Root
The Result or answer when adding the digits of a number together. In the exapmle above, 4896 = 9. Nine is the Digital Root.
Pythagorean Math
this is the place to put the definition of pythagorean math
Gematria / Ciphers
Gematria
Definition of gematria
Cipher
definition of cipher
Hebrew Ciphers Used on this Site.
Mispar Hechrechi (Standard Value) – Each Hebrew letter is assigned its basic numerical value from 1 to 400. Used on this site for interpretive meaning, scripture connections, and booklet notes.
| Letter, Name, Value | Letter, Name, Value | Letter, Name, Value |
| א (Aleph) = 1 | י (Yod) = 10 | ק (Qof)=100 |
| ב (Bet) = 2 | כ/ך (Kaf) = 20 | ר (Resh) = 200 |
| ג (Gimel) = 3 | ל (Lamed) = 30 | ש (Shin)= 300 |
| ד (Dalet) = 4 | מ/ם (Mem) = 40 | ת (Tav) = 400 |
| ה (Heh) = 5 | נ/ן (Nun) = 50 | |
| ו (Vav) = 6 | ס (Samekh) = 60 | |
| ז (Zayin) = 7 | ע (Ayin) = 70 | |
| ח (Chet) = 8 | פ/ף (Pe) = 80 | |
| ט (Tet) = 9 | צ/ץ (Tzadi) = 90 |
Mispar Gadol (Final-Form Expansion) – Same as Standard Value, except final-form letters take expanded values (500–900). Used on this site for the 3-letter Hebrew Seals because it represents the mature or activated form of the number.
| Final Letter | Standard Value | Extended (Gadol) Value |
| ך (Final Kaf) | 20 | 500 |
| ם (Final Mem) | 40 | 600 |
| ן (Final Nun) | 50 | 700 |
| ף (Final Pe) | 80 | 800 |
| ץ (Final Tzadi) | 90 | 900 |
Music
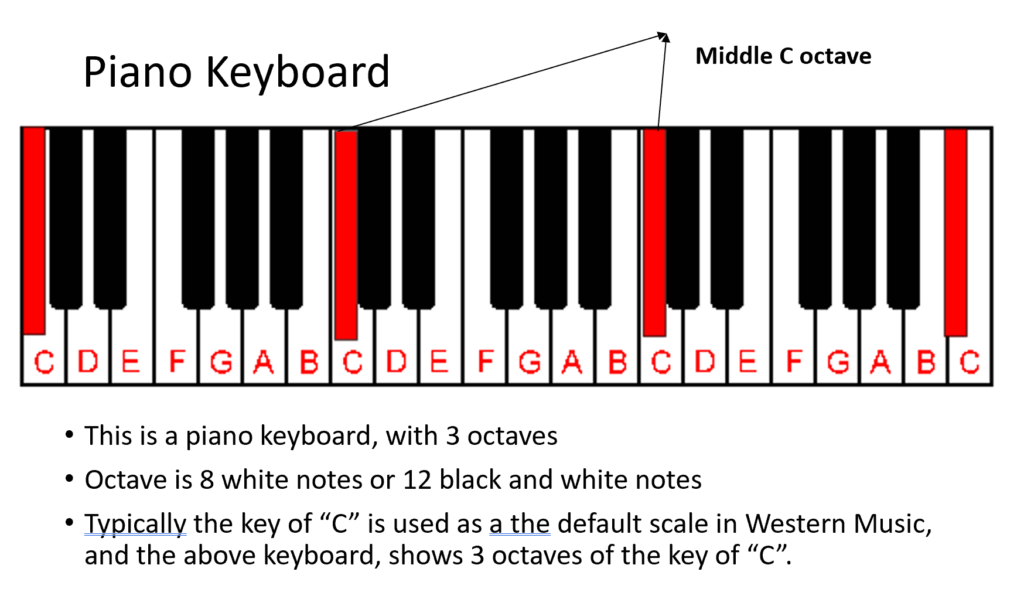
Chromatic Scale
The Chromatic scale is the combination of all the notes in an Octave, both black and white notes.
The twelve notes of the octave—all the black and white keys in one octave on the piano—form the chromatic scale. The tones of the chromatic scale (unlike those of the major or minor scale) are all the same distance apart, one half step. The word chromatic comes from the Greek chroma, color; and the traditional function of the chromatic scale is to color or embellish the tones of the major and minor scales. It does not define a key, but it gives a sense of motion and tension. It has long been used to evoke grief, loss, or sorrow. In the twentieth century it has also become independent of major and minor scales and is used as the basis for entire compositions.
Diatonic Scale
The Diatonic scale is the white notes of an Octave.
Equal Temperament
“An equal temperament is a musical temperament or tuning system that approximates just intervals by dividing an octave (or other interval) into steps such that the ratio of the frequencies of any adjacent pair of notes is the same. This system yields pitch steps perceived as equal in size, due to the logarithmic changes in pitch frequency.” – Wikipedia
“An equal temperament is a musical temperament or tuning system that approximates just intervals by dividing an octave (or other interval) into steps such that the ratio of the frequencies of any adjacent pair of notes is the same. This system yields pitch steps perceived as equal in size, due to the logarithmic changes in pitch frequency.” – Wikipedia
Just Intonation
In music, just intonation or pure intonation is a tuning system in which the space between notes’ frequencies (called intervals) is a whole number ratio. Intervals spaced in this way are said to be pure, and are called just intervals. Just intervals (and chords created by combining them) consist of tones from a single harmonic series of an implied fundamental.
Law of the Octave
The Law of the Octave states: When you multiply a frequency (in Hz) by 2, you get the same note only an octave higher. When you divide a frequency by 2, you get the same note only an octave lower.
Scale
In music theory, a scale is “any consecutive series of notes that form a progression between one note and its octave”, typically by order of pitch or fundamental frequency.
Solfeggio
From Wikipedia: “In music, solfège (/ˈsɒlfɛʒ/, French: [sɔlfɛʒ]) or solfeggio (/sɒlˈfɛdʒioʊ/; Italian: [solˈfeddʒo]), also called sol-fa, solfa, solfeo, among many names, is a mnemonic used in teaching aural skills, pitch and sight-reading of Western music. Solfège is a form of solmization, though the two terms are sometimes used interchangeably.
Syllables are assigned to the notes of the scale and assist the musician in audiating, or mentally hearing, the pitches of a piece of music, often for the purpose of singing them aloud. Through the Renaissance (and much later in some shapenote publications) various interlocking four-, five- and six-note systems were employed to cover the octave. The tonic sol-fa method popularized the seven syllables commonly used in English-speaking countries: do (spelled doh in tonic sol-fa),[1] re, mi, fa, so(l), la, and ti (or si). There are two current ways of applying solfège: 1) fixed do, where the syllables are always tied to specific pitches (e.g., “do” is always “C-natural”) and 2) movable do, where the syllables are assigned to scale degrees, with “do” always the first degree of the major scale.”